1. 단항 선형 회귀
* 한 개의 입력이 들어가서 한 개의 출력이 나오는 구조
import torch
import torch.nn as nn
import torch.optim as optim
import matplotlib.pyplot as plt
# 랜덤 값 고정
torch.manual_seed(2024)
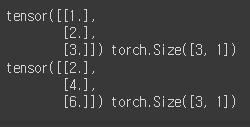
x_train = torch.FloatTensor([[1], [2], [3]])
y_train = torch.FloatTensor([[2], [4], [6]])
print(x_train, x_train.shape)
print(y_train, y_train.shape)
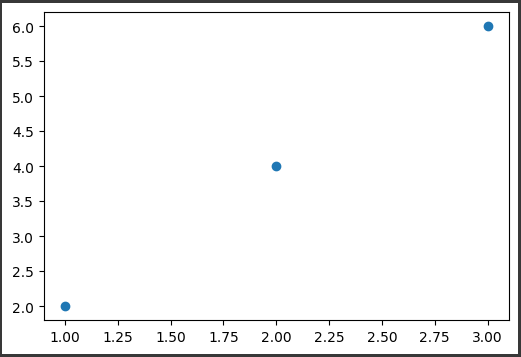
plt.figure(figsize=(6, 4))
plt.scatter(x_train, y_train)
# y = wx + b
model = nn.Linear(1, 1)
y_pred = model(x_train)
list(model.parameters())
# MSE 실제 식과 메서드 사용
((y_pred - y_train) ** 2 ).mean()
loss = nn.MSELoss()(y_pred, y_train)
loss
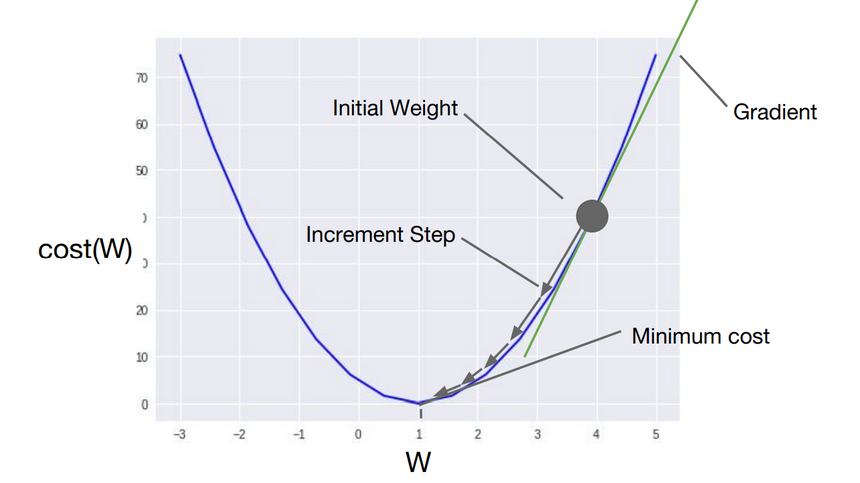
2. 경사하강법(Gradient Descent)
* 비용함수의 값을 최소로 하는 W와 b를 찾는 알고리즘을 '옵티마이저 알고리즘' 이라고 함
* 옵티마이저 알고리즘 중 가장 기본적인 기술이 경사하강법
* 옵티마이저 알고리즘을 통해 W와 b를 찾아내는 과정을 "학습" 이라고 부름
* 학습률(Learning rate) : 한 번 W를 움직이는 거리(increment step)
# SGD(Stochastic Gradient Descent)
# 랜덤하게 데이터를 하나씩 뽑아서 loss를 만듦
# 데이터를 뽑고 다시 데이터에 넣고 반복
# 빠르게 방향을 결정
optimizer = optim.SGD(model.parameters(), lr=0.01)
loss = nn.MSELoss()(y_pred, y_train)
# gradient를 초기화
optimizer.zero_grad()
# 역전파: 비용 함수를 미분하여 gradient(기울기) 계산
loss.backward()
# W와 b를 업데이트
optimizer.step()
print(list(model.parameters())) # W : 0.2177, b: 0.7267
# 반복 학습을 통해 오차가 있는 W, b를 수정하면서 오차를 계속 줄여나감
# epochs: 반복 학습 횟수(에포크)
epochs = 1000
for epoch in range(epochs + 1):
y_pred = model(x_train)
loss = nn.MSELoss()(y_pred, y_train)
optimizer.zero_grad()
loss.backward()
optimizer.step()
if epoch % 100 == 0 :
print(f'Epoch: {epoch}/{epochs} Loss: {loss:.6f}')
print(list(model.parameters())) # W : 1.9499, b: 0.1138
#test
x_test = torch.FloatTensor([[5]])
y_pred = model(x_test)
print(y_pred)
3. 다중 선형 회귀
* 여러 개의 입력이 들어가서 한 개의 출력이 나오는 구조
X_train = torch.FloatTensor([[73, 80, 75],
[93, 88, 93],
[89, 91, 90],
[96, 98, 100],
[73, 66, 70]])
y_train = torch.FloatTensor([[150], [190], [180], [200], [130]])
print(X_train, X_train.shape)
print(y_train, y_train.shape)
# y = Wx + b 단항 선형 회귀
# y = W1x1 + W2x2 + W3x3 ... + b 다중 선형 회귀
model = nn.Linear(3,1)
print(model)
epochs = 10000
for epoch in range(epochs + 1):
y_pred = model(X_train)
loss = nn.MSELoss()(y_pred, y_train)
optimizer.zero_grad()
loss.backward()
optimizer.step()
if epoch % 100 == 0 :
print(f'Epoch: {epoch}/{epochs} Loss: {loss:.6f}')
optimizer = optim.SGD(model.parameters(), lr=0.00001)
print(list(model.parameters()))
# 93, 93, 93
x_test = torch.FloatTensor([[93, 93, 93]])
y_pred = model(x_test)
print(y_pred)
4. temps.csv 데이터에서 기온에 따른 지면 온도를 예측해보기
import pandas as pd
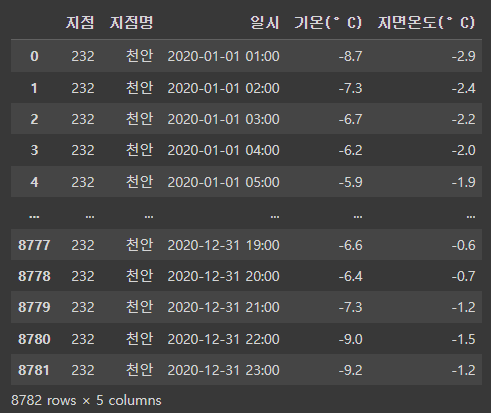
df = pd.read_csv('/content/drive/MyDrive/KDT 국비지원/6. 머신러닝과 딥러닝/Data/temps.csv', encoding = 'euc-kr')
df
x_data = df[['기온(°C)']]
y_data = df[['지면온도(°C)']]
# x_data 가 df 형식이니 values를 가져와야함
x_data = torch.FloatTensor(x_data.values)
y_data = torch.FloatTensor(y_data.values)
print(x_data.shape)
print(y_data.shape)
plt.figure(figsize=(8, 6))
plt.scatter(x_data, y_data)
model = nn.Linear(1, 1)
optimizer = torch.optim.SGD(model.parameters(), lr = 0.001)
print(list(model.parameters())) # W : - 0.5700, b : 0.2403
epochs = 10000
for epoch in range(epochs + 1) :
y_pred = model(x_data)
loss = nn.MSELoss()(y_pred, y_data)
optimizer.zero_grad()
loss.backward()
optimizer.step()
if epoch % 100 == 0 :
print(f'Epoch : {epoch}/{epochs} Loss : {loss:.6f}')
# tensor 형을 numpy로 바꿔야함
y_pred = model(x_data).detach().numpy()
y_pred
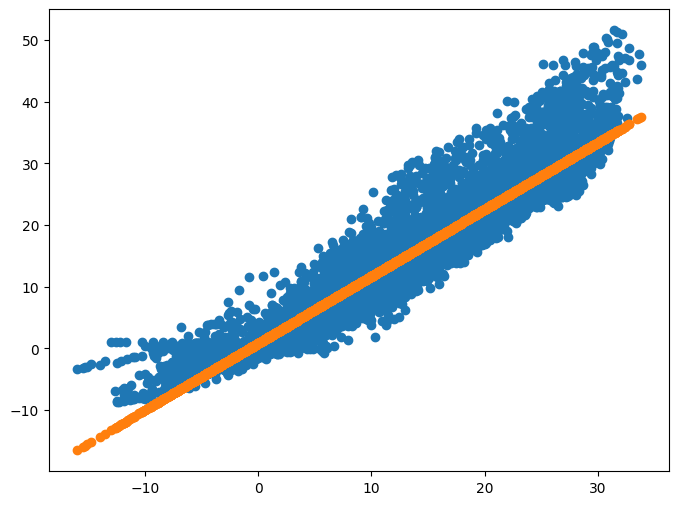
plt.figure(figsize=(8, 6))
plt.scatter(x_data, y_data)
plt.scatter(x_data, y_pred)
# 온도가 26도일때 지면온도는 몇도일까? 예측
result = model(torch.FloatTensor([[26]]))
result
'딥러닝과 머신러닝' 카테고리의 다른 글
| Data Loader(2024-06-20) (0) | 2024.06.20 |
|---|---|
| Pytorch로 구현한 논리회귀 (2024-06-20) 미완성 (0) | 2024.06.20 |
| KMean, Silhouette Score (2024-06-18) (0) | 2024.06.18 |
| 여러 모델 적용 후 성능 확인하기 (2024-06-18) (0) | 2024.06.18 |
| lightGBM (2024-06-18) (0) | 2024.06.18 |



