1. 비선형 활성화 함수 (Activation Funtions)
* 신경망의 성능을 향상시키기 위해 사용
* 선형 함수는 입력값과 가중치를 곱한 결과를 그대로 출력하기 때문에 신경망에서 여러개의 레이어를 사용한다면 최종 출력값은 입력 값과 가중치의 선형 조합으로 표현되므로 입력 데이터를 비선형 관게를 표현할 수 없음
* 신경망이 입력 데이터의 비선형 관계를 잘 학습할 수 있도록 하기 위해 비선형 활성화 함수가 필요하다




2. 역전파(Backpropagaion)
* 1969년 민스키 교수님 XOR는 "지금의 기술로 풀 수 없다"라는 것을 수학적으로 증명했다
* 1974년 Paul Werbos에 의해 박사 논문에서 해결됨
* W, b를 이용해 주어진 입력을 가지고 출력을 만들어 낼 수 있음 -> 출력이 우리가 가지고 있는 값과 다른 출력일 경우 W,b를 조절함
* 1986년 Hinton에 의해 위 같은 방법으로 독자적으로 만들어 냄(재발견)
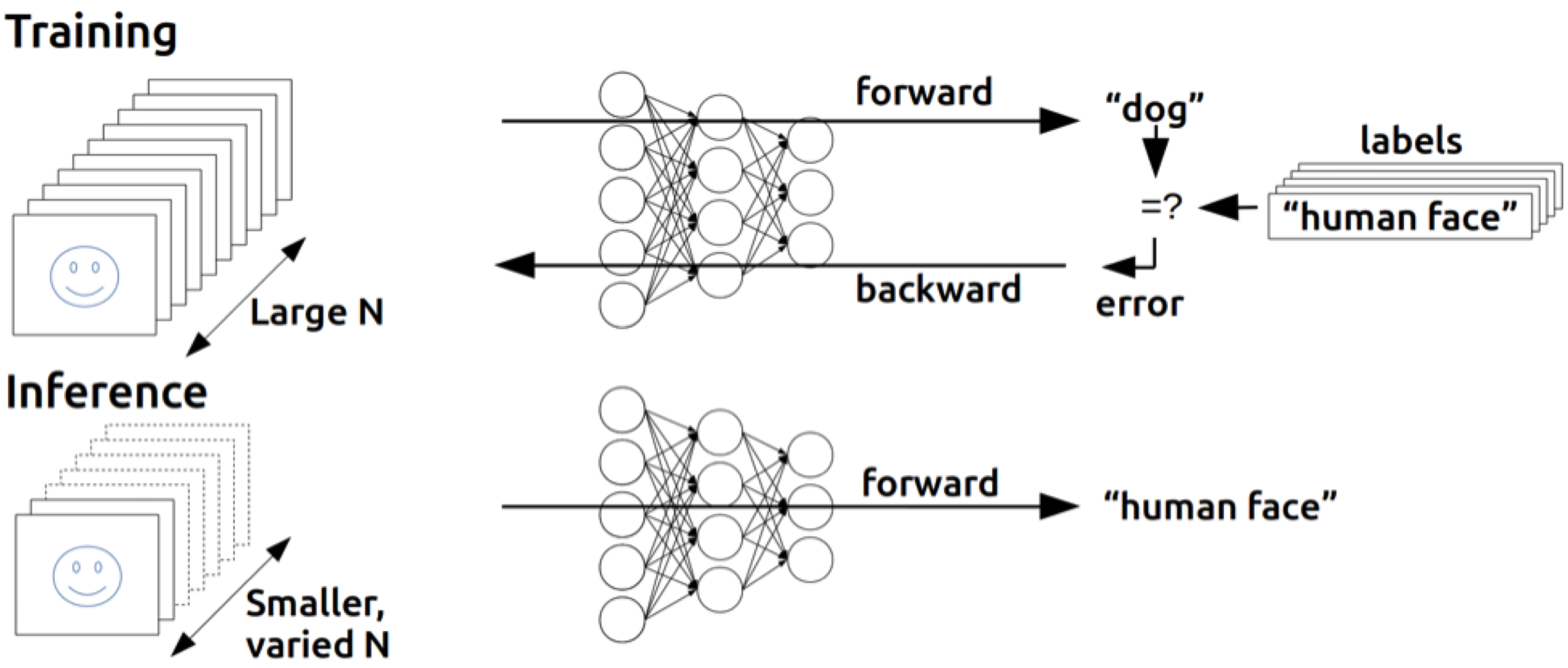
* 역전파는 인공신경망에서 학습을 수행하는 데 사용되는 알고리즘으로, 네트워크의 가중치를 업데이트 하기위해 오차를 출력층에서 입력층으로 전파하여 각 가중치의 기울기를 계산
* 신경망이 주어진 데이터에 대해 예측을 얼마나 잘하는지 평가하고 네트워크의 가중치를 조정하여 예측 성능을 향상시키는 중요한 과정
* 역전파 알고리즘 단계
1. 순전파 계산
* 입력 데이터를 각 층을 통과시키면서 네트워크의 출력을 계산한다
* 출력층에서 손실 함수를 사용하여 출력과 실제 값의 오차를 계산
2. 오차 계산
* 출력층에서 시작하여 이전 층으로 이동하며 오차를 계산
* 출력층의 오차는 손실 함수의 미분으로 구함
3. 기울기 계산
* 각 층에서 가중치와 바이어스에 대한 기울기를 계산
* 기울기는 오차와 활성화 함수의 미분을 사용하여 구함
4. 가중치 업데이트
* 경사 하강법을 사용하여 가중치와 바이어스를 업데이트 함
'딥러닝과 머신러닝' 카테고리의 다른 글
| 간단한 CNN model 만들기 (2024-06-20) (0) | 2024.06.20 |
|---|---|
| CNN(Convolutional Neural Networks) (2024-06-20) (0) | 2024.06.20 |
| neuron, Perceptron (2024-06-20) (0) | 2024.06.20 |
| Data Loader(2024-06-20) (0) | 2024.06.20 |
| Pytorch로 구현한 논리회귀 (2024-06-20) 미완성 (0) | 2024.06.20 |



