1. 뉴런(neuron)
* 인간의 뇌는 수십억 개의 뉴런을 가지고 있음
* 뉴런은 화학적, 전기적 신호를 처리하고 전달하는 연결된 뇌 신경 세포

1-2. 인공 뉴런
* 1943년에 워렌 맥컬록, 월터 피츠가 단순화된 뇌 세포 개념을 발표
* 신경 세포를 이진 출력을 가진 단순한 논리 게이트라고 설명
* 생물학적 뉴런의 모델에 기초한 수하적 기능으로 각 뉴런이 입력을 받아 개별적으로 가중치를 곱하여 나온 합계를 비선형 함수를 전달하여 출력을 생성
2. 퍼셉트론(Perceptron)
* 인공 신경망의 가장 기본적인 형태로 1957년에 처음 소개됨
* 입력과 출력을 가진 단일 뉴런 모델을 기반으로 만듬
* 초기에 기계 학습 알고리즘 중 하나로 이진 분류 문제를 해결하기 위해 설계
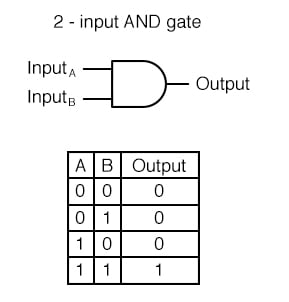
2-1. 논리 회귀(단층 퍼셉트론)로 AND 문제 풀기
import torch
import torch.nn as nn
import torch.optim as optim
X = torch.FloatTensor([[0, 0], [0, 1], [1, 0], [1, 1]])
y = torch.FloatTensor([[0], [0], [0], [1]])
model = nn.Sequential(
nn.Linear(2, 1),
nn.Sigmoid())
optimizer = optim.SGD(model.parameters(), lr=1)
epochs = 1000
for epoch in range(epochs + 1):
y_pred = model(X)
loss = nn.BCELoss()(y_pred, y)
optimizer.zero_grad()
loss.backward()
optimizer.step()
if epoch % 100 == 0:
y_bool = (y_pred >=0.5).float()
accuracy = (y_bool == y).float().sum() / len(y) * 100
print(f'Epoch: {epoch:4d}/{epochs}, Loss: {loss:.6f}, Accuracy: {accuracy:.2f}%')
2-2. 논리 회귀(단층 퍼셉트론)으로 OR문제 풀기
X = torch.FloatTensor([[0, 0], [0, 1], [1, 0], [1, 1]])
y = torch.FloatTensor([[0], [1], [1], [1]])
model = nn.Sequential(
nn.Linear(2, 1),
nn.Sigmoid()
)
optimizer = optim.SGD(model.parameters(), lr=1)
epochs = 1000
for epoch in range(epochs + 1):
y_pred = model(X)
loss = nn.BCELoss()(y_pred, y)
optimizer.zero_grad()
loss.backward()
optimizer.step()
if epoch % 100 == 0:
y_bool = (y_pred >= 0.5).float()
accuracy = (y == y_bool).float().sum() / len(y) * 100
print(f'Epoch {epoch:4d}/{epochs} Loss: {loss:.6f} Accuracy: {accuracy:.2f}%')
2-3. 논리 회귀(단층 퍼셉트론)로 XOR 문제 풀기

X = torch.FloatTensor([[0, 0], [0, 1], [1, 0], [1, 1]])
y = torch.FloatTensor([[0], [1], [1], [0]])
model = nn.Sequential(
nn.Linear(2, 1),
nn.Sigmoid()
)
optimizer = optim.SGD(model.parameters(), lr=1)
epochs = 1000
for epoch in range(epochs + 1):
y_pred = model(X)
loss = nn.BCELoss()(y_pred, y)
optimizer.zero_grad()
loss.backward()
optimizer.step()
if epoch % 100 == 0:
y_bool = (y_pred >= 0.5).float()
accuracy = (y == y_bool).float().sum() / len(y) * 100
print(f'Epoch {epoch:4d}/{epochs} Loss: {loss:.6f} Accuracy: {accuracy:.2f}%')
2-4. 다층 퍼셉트론으로 XOR 문제 풀기
* 여러개의 은닉층을 만들어 해결하기
model = nn.Sequential(
nn.Linear(2, 64),
nn.Sigmoid(),
nn.Linear(64, 32),
nn.Sigmoid(),
nn.Linear(32, 16),
nn.Sigmoid(),
nn.Linear(16, 1),
nn.Sigmoid()
)
print(model)
X = torch.FloatTensor([[0, 0], [0, 1], [1, 0], [1, 1]])
y = torch.FloatTensor([[0], [1], [1], [0]])
optimizer = optim.SGD(model.parameters(), lr=1)
epochs = 5000
for epoch in range(epochs + 1):
y_pred = model(X)
loss = nn.BCELoss()(y_pred, y)
optimizer.zero_grad()
loss.backward()
optimizer.step()
if epoch % 100 == 0:
y_bool = (y_pred >= 0.5).float()
accuracy = (y == y_bool).float().sum() / len(y) * 100
print(f'Epoch {epoch:4d}/{epochs} Loss: {loss:.6f} Accuracy: {accuracy:.2f}%')
'딥러닝과 머신러닝' 카테고리의 다른 글
| CNN(Convolutional Neural Networks) (2024-06-20) (0) | 2024.06.20 |
|---|---|
| Activation Functions, Backpropagaion(2024-06-20) (0) | 2024.06.20 |
| Data Loader(2024-06-20) (0) | 2024.06.20 |
| Pytorch로 구현한 논리회귀 (2024-06-20) 미완성 (0) | 2024.06.20 |
| Pytorch 선형회귀(2024-06-19) (1) | 2024.06.20 |



