1. hr 데이터셋
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
hr_df = pd.read_csv('/content/drive/MyDrive/KDT 국비지원/6. 머신러닝과 딥러닝/Data/hr.csv')
hr_df.head()
* employee_id: 임의의 직원 아이디
* department: 부서
* region: 지역
* education: 학력
* gender: 성별
* recruitment_channel: 채용 방법
* no_of_trainings: 트레이닝 받은 횟수
* age: 나이
* previous_year_rating: 이전 년도 고과 점수
* length_of_service: 근속 년수
* awards_won: 수상 경력
* avg_training_score: 평균 고과 점수
* is_promoted: 승진 여부
목표 : 승진에 영향을 미치는 요소들을 확인하고 데이터 일부를 학습한 후 나머지 데이터로 승진 가능성 예측
# 지난해 고과점수와 승진의 연관성
sns.barplot(x='previous_year_rating', y='is_promoted', data=hr_df)
sns.lineplot(x='previous_year_rating', y='is_promoted', data=hr_df)
# 평균 고과 점수와 승진의 연관성
sns.lineplot(x='avg_training_score', y='is_promoted', data=hr_df)
# 세로 줄이 길면 데이터의 수가 적어 판단하기 어렵다는 뜻
sns.barplot(x='recruitment_channel', y='is_promoted', data=hr_df)
hr_df['recruitment_channel'].value_counts()
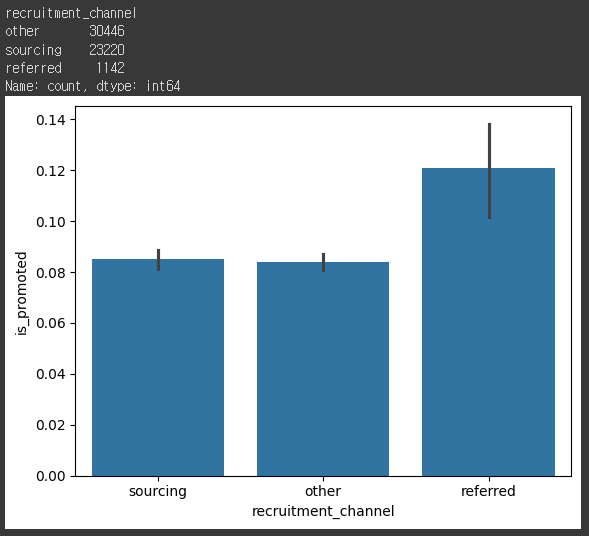
# 데이터가 많아서 null값 그냥 드랍하고 진행
hr_df = hr_df.dropna()
# 원 핫 인코딩 이전에 열의 고유 값 개수 파악
for i in ['department', 'region', 'education', 'gender', 'recruitment_channel']:
print(i, hr_df[i].nunique())
# 원 핫 인코딩
hr_df = pd.get_dummies(hr_df, columns = ['department', 'education', 'gender', 'recruitment_channel'] )
hr_df.head()
hr_df.drop(['employee_id', 'region'], axis=1, inplace=True)
X_train, X_test, y_train, y_test = train_test_split(hr_df.drop('is_promoted', axis=1), hr_df['is_promoted'], test_size=0.2, random_state=2024)
X_train.shape, X_test.shape, y_train.shape, y_test.shape
2. 로지스틱 회귀(Logistic Regression)
* 둘 중의 하나를 결정하는 문제(이진 분류)를 풀기 위한 대표적인 알고르짐
* 입력 데이터와 가중치의 선형 조합으로 선형 방정식을 만듦 -> 선형 방적식의 결과를 0과 1사이의 확률 값으로 변환(시그모이드 함수)
* 3개 이상의 클래스에 대한 판별도 할 수 있음
* OvR(One-vs-Rest) : 각 클래스마다 하나의 이진 분류기를 만들고, 해당 클래스를 기준으로 그 클래스와 나머지 모든 클래스를 구분하는 이진 분류를 실행 -> 가장 높은 확률을 가진 클래스를 선택
* OvO(One-vs-One) : 클래스의 개수가 N인 경우 N(N-1)/2 개의 이진 분류기를 만듦 -> 입력 데이터를 각 이진 분류기에 넣어 가장 많이 선택된 클래스를 최종 선택
> 대부분 OvR 전략을 선호하는데, 클래스 간의 구분이 명확하지 않거나 데이터가 한쪽으로 치우친 경우 OvO를 고려한다.
from sklearn.metrics import accuracy_score, confusion_matrix
from sklearn.linear_model import LogisticRegression
lr = LogisticRegression()
lr.fit(X_train, y_train) # 학습
pred = lr.predict(X_test) # 예측
accuracy_score(y_test, pred) # 모델 성능 평가
3. 혼돈 행렬(confusion matrix)
* 정밀도와 재현율(민감도)을 활용하는 평가용 지수
* TN : 승진하지 못했는데, 승진하지 못했다고 예측
* FP : 승진했는데 승진하지, 못했다고 예측
* FN : 승잔하지 못했는데, 승진했다고 예측
* TP : 승진했는데, 승진했다고 예측
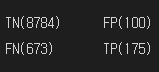
confusion_matrix(y_test, pred)
# array ([[8784, 100],
# [ 673, 175]])
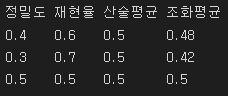
3-1. 정밀도(Precision)
* TP / (TP + FP)
* 무조건 양성으로 판단해서 계산하는 방법
* 실제 1인 것 중에서 얼마 만큼을 제대로 맞췄는가?
3-2. 재현율(recall)
* TP / (TP + FN)
* 정확하게 감지한 양성 샘플의 비율
* 1이라고 예측한 것 중, 얼마만큼을 제대로 맞췄는가?
* 민감도 또는 TPR(True Positive Rate)라고도 부름
3-3. f1 score
* 정밀도와 재현율의 조화평균을 나타내는 지표

from sklearn.metrics import precision_score, recall_score, f1_score
precision_score(y_test, pred)
# 0.6363636363636364
recall_score(y_test, pred)
#0.20636792452830188
f1_score(y_test, pred)
#0.31166518254674974
lr.coef_ # 각 독립변수의 기울기 # 종속변수 is_promoted를 제외한 23개 열
([[-0.51687179, -0.06608108, 0.38010122, 0.05941589, 3.53168128,
0.11251127, -1.95349302, -0.35850951, -0.39898613, -0.3578027 ,
0.49199051, -0.28645626, -1.19810409, 1.53916888, -1.24856123,
-1.65001362, -1.02150699, -1.09923293, -1.80257786, -1.96817568,
-1.67721465, -0.44336313, -1.65017577]])
# 독립변수
tempX = hr_df[['previous_year_rating', 'avg_training_score', 'awards_won?']]
# 종속변수
tempy = hr_df['is_promoted']
# 객체 생성
temp_lr = LogisticRegression()
# 학습
temp_lr.fit(tempX, tempy)
# temp df 생성
temp_df = pd.DataFrame({
'previous_year_rating':[4.0, 5.0, 5.0],
'avg_training_score':[100, 90, 100],
'awards_won?':[0, 0, 1]
})
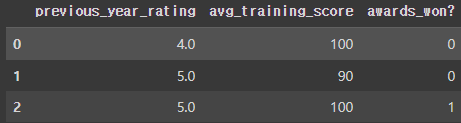
# 예측
pred = temp_lr.predict(temp_df)
# 예측 결과 index2만 승진 가능
pred
array([0, 0, 1])
temp_lr.coef_ # 기울기
array([[0.51112537, 0.04309755, 2.09583168]])
temp_lr.intercept_ # 절편
array([-7.20658921])
proba = temp_lr.predict_proba(temp_df)
proba
array([[0.70105625, 0.29894375],
[0.6839929 , 0.3160071 ],
[0.14746488, 0.85253512]])
# 임계값 설정
# 일반적인 기본 임계값은 0.5
# 0.5보다 크면 1(True) 작으면 0(False)로 구분한다
threshold = 0.5
pred = (proba > threshold).astype(int)
pred
array([0, 0, 1])
4. 교차 검증(Cross Validation)
* train_test_split에서 발생하는 데이터의 섞임에 따라 성능이 좌우되는 문제를 해결하기 위한 방법
* K겹(K-Fold) 교차 검증을 가장 많이 사용
from sklearn.model_selection import KFold
kf= KFold(n_splits=5)
kf
for train_index, test_index in kf.split(range(len(hr_df))):
print(train_index, test_index, len(train_index), len(test_index))
# random state가 없는 상태
# train_index test_index len(train_index) len(test_index)
# [ 9732 9733 9734 ... 48657 48658 48659] [ 0 1 2 ... 9729 9730 9731] 38928 9732
# [ 0 1 2 ... 48657 48658 48659] [ 9732 9733 9734 ... 19461 19462 19463] 38928 9732
# [ 0 1 2 ... 48657 48658 48659] [19464 19465 19466 ... 29193 29194 29195] 38928 9732
# [ 0 1 2 ... 48657 48658 48659] [29196 29197 29198 ... 38925 38926 38927] 38928 9732
# [ 0 1 2 ... 38925 38926 38927] [38928 38929 38930 ... 48657 48658 48659] 38928 9732
kf= KFold(n_splits=5, random_state=2024, shuffle=True)
kf
for train_index, test_index in kf.split(range(len(hr_df))):
print(train_index, test_index, len(train_index), len(test_index))
# [ 1 2 3 ... 48656 48658 48659] [ 0 7 8 ... 48638 48640 48657] 38928 9732
# [ 0 1 5 ... 48656 48657 48658] [ 2 3 4 ... 48647 48652 48659] 38928 9732
# [ 0 1 2 ... 48657 48658 48659] [ 6 16 18 ... 48654 48655 48656] 38928 9732
# [ 0 1 2 ... 48656 48657 48659] [ 5 14 15 ... 48645 48650 48658] 38928 9732
# [ 0 2 3 ... 48657 48658 48659] [ 1 10 13 ... 48642 48649 48651] 38928 9732
# KFold(n=5)를 사옹하여 위 데이터를 LogisticRegression 모델로 학습을 시키고
# 각 n마다 예측결과를 accuracy_score 값으로 출력
acc_list = []
for train_index, test_index in kf.split(range(len(hr_df))):
X = hr_df.drop('is_promoted', axis=1)
y = hr_df['is_promoted']
X_train = X.iloc[train_index]
X_test = X.iloc[test_index]
y_train = y.iloc[train_index]
y_test = y.iloc[test_index]
lr = LogisticRegression()
lr.fit(X_train, y_train)
pred = lr.predict(X_test)
acc_list.append(accuracy_score(y_test, pred))
acc_list
[0.9202630497328401,
0.9217016029593095,
0.9324907521578298,
0.9276613234689683,
0.9189272503082614]
np.array(acc_list).mean()
0.9242087957254418
크로스밸리데이션을 사용하는 이유는 결과를 좋게하기 위함이 아니라, 믿을만한 검증을 하기 위함
'딥러닝과 머신러닝' 카테고리의 다른 글
| Random Forest, 하이퍼파라미터, Feature Importances (0) | 2024.06.17 |
|---|---|
| Scaling, Normalization, Support Vector Machine (2024-06-12) (0) | 2024.06.17 |
| Linear Regression, MSE, MAE, RMSE(2024-06-11) (0) | 2024.06.11 |
| 타이타닉 데이터셋(2024-06-10) (0) | 2024.06.10 |
| iris-data (2024-06-10) (0) | 2024.06.10 |



