1. Rent 데이터셋
import numpy as np
import pandas as pd
import seaborn as sns
데이터 설정
rent_df = pd.read_csv('/content/drive/MyDrive/KDT 국비지원/6. 머신러닝과 딥러닝/Data/rent.csv')
rent_df.head()

rent_df.info()


round(rent_df.describe(), 2) # 소수점 2자리까지 반올림

rent_df['Rent'].sort_values()

sns.boxplot(rent_df['Rent'])

rent_df.isna().sum() # null값 확인

rent_df.dropna(subset= ['BHK']) # BHK 값이 null인 데이터를 삭제
na_index = rent_df[rent_df['Size'].isna()].index # Size값이 null인 index값
na_index

rent_df['Size'].fillna(rent_df['Size'].median()).loc[na_index]

rent_df.info()
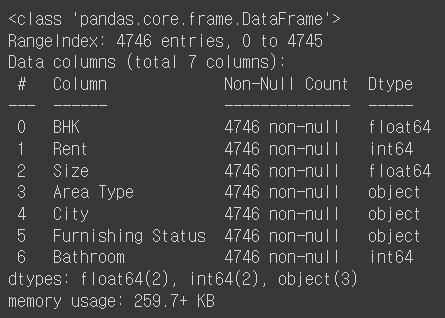
rent_df = pd.get_dummies(rent_df, columns=['Area Type', 'City', 'Furnishing Status'])

# 차원이 있는 행렬값은 대문자
# 1차원은 소문자 (리스트여도)
# 관례적임
X = rent_df.drop('Rent',axis=1) # 독립변수
y = rent_df['Rent'] # 종속변수
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=2024)
X_train.shape, X_test.shape, y_train.shape, y_test.shape

2. 선형 회귀(Linear Regression)
* 데이터를 통해 데이터를 가장 잘 설명할 수 있는 직선으로 데이터를 분석하는 방법
* 단순 선형 회귀분석(단일 독립변수를 이용)
* 다중 선형 회귀분석(다중 독립변수를 이용)
from sklearn.linear_model import LinearRegression
lr = LinearRegression() #객체
lr.fit(X_train, y_train) #학습
pred = lr.predict(X_test)
3. 평가지표 만들기
3-1. MSE(Mean Squared Error)
* 예측값과 실제값의 차이에 대한 제곱에 대해 평균을 낸 값

* 실제값이 예측값보다 클 수도 작을 수도 있으니 제곱을 안하면 음수/양수 구분이 안됨
p = np.array([3, 4, 5]) # 예측값
act = np.array([1, 2, 3]) # 실제값
def my_mse(pred, actual):
return ((pred- actual) **2).mean()
my_mse(p, act) # 4.0
3-2. MAE(Mean Absolute Error)
* 예측값과 실제값의 차이에 대한 절대값에 대해 평균을 낸 값

* 오차 값을 줄이기 위해 기울기를 수정하는 과정에서 미분 연산을 하는데 절대값은 미분이 어렵기 때문에 잘 사용하지 않음
* 장점 : 제곱을 하지 않기 때문에 숫자가 작아서 컴퓨터가 연산할 때 부담이 적다
# abs = 절대값
def my_mae(pred, actual):
return np.abs(pred - actual).mean()
my_mae(p, act)
3-3. RMSE(Root Mean Squared Error)
* 예측값과 실제값의 차이에 대한 제곱에 대해 평균을 낸 후 루트를 씌운 값
*

# sqrt = 루트 / squared true 인것 같은
def my_rmse(pred, actual):
return np.sqrt(my_mse(pred, actual))
my_rmse(p, act)
from sklearn.metrics import mean_absolute_error, mean_squared_error
mean_absolute_error(p, act) # MAE 2.0
mean_squared_error(p, act) # MSE 4.0
mean_squared_error(p, act, squared=False) # RMSE 2.0
3-4. 데이터에 평가 지표 적용하기
mean_squared_error(y_test, pred) # 1426204740.330996
mean_absolute_error(y_test, pred) # 21997.237341647397
mean_squared_error(y_test, pred, squared=False) # 37765.125980605386
# 아웃라이어로 생각되는 데이터를 삭제 시킨 후 학습을 다시하고 평가지표 변화 체크
X_train.drop(1837, inplace=True)
y_train.drop(1837, inplace=True)
# 1837이 train 즉 학습하는 데이터 안에 있다면 실행이 되고 오류가 발생하면 X_test안에 들어있었을 것
lr.fit(X_train, y_train) #다시 학습
pred = lr.predict(X_test)
mean_squared_error(y_test, pred, squared=False) # 37731.275512059074
# 1837 삭제전 : 37765.125980605386
# 1837 삭제후 : 37731.275512059074
37765.125980605386 - 37731.275512059074
# 33.850468546312186 만큼 오차가 줄었음
'딥러닝과 머신러닝' 카테고리의 다른 글
| Scaling, Normalization, Support Vector Machine (2024-06-12) (0) | 2024.06.17 |
|---|---|
| Logistic Regression(2024-06-12) (1) | 2024.06.12 |
| 타이타닉 데이터셋(2024-06-10) (0) | 2024.06.10 |
| iris-data (2024-06-10) (0) | 2024.06.10 |
| Scikit-Learn(2024-06-10) (0) | 2024.06.10 |



